Definición 1
Es determinar la dimensión de la magnitud de una variable en relación con una unidad de medida preestablecida y convencional.
Se conocen algunos sistemas convencionales para establecer las unidades de medida: El Sistema Internacional y el Sistema Inglés.
Definición 2
Es comparar la cantidad desconocida que queremos determinar y una cantidad conocida de la misma magnitud, que elegimos como unidad. Teniendo como punto de referencia dos cosas: un objeto (lo que se quiere medir) y una unidad de medida ya establecida ya sea en Sistema Inglés, Sistema Internacional, o una unidad arbitraria.
Al resultado de medir lo llamamos Medida.
Cuando medimos algo se debe hacer con gran cuidado, para evitar alterar el sistema que observamos. Por otro lado, no hemos de perder de vista que las medidas se realizan con algún tipo de error, debido a imperfecciones del instrumental o a limitaciones del medidor, errores experimentales, por eso, se ha de realizar la medida de forma que la alteración producida sea mucho menor que el error experimental que se pueda cometer.
Unidades de medida
Al patrón de medir le llamamos también Unidad de medida.
Debe cumplir estas condiciones:
1º.- Ser inalterable, esto es, no ha de cambiar con el tiempo ni en función de quién realice la medida.
2º.- Ser universal, es decir utilizada por todos los países.
3º.- Ha de ser fácilmente reproducible.
Reuniendo las unidades patrón que los científicos han estimado más convenientes, se han creado los denominados Sistemas de Unidades.
Sistema Internacional ( S.I.)
Este nombre se adoptó en el año 1960 en la XI Conferencia General de Pesos y Medidas, celebrada en París buscando en él un sistema universal, unificado y coherente que toma como Magnitudes fundamentales: Longitud, Masa, Tiempo, Intensidad de corriente eléctrica, Temperatura termodinámica, Cantidad de sustancia, Intensidad luminosa. Toma además como magnitudes complementarias: Angulo plano y Angulo sólido.
Medida directa
La medida o medición diremos que es directa, cuando disponemos de un instrumento de medida que la obtiene, así si deseamos medir la distancia de un punto a a un punto b, y disponemos del instrumento que nos permite realizar la medición, esta es directa.Errores en las medidas directas
El origen de los errores de medición es muy diverso, pero podemos distinguir:
* Errores sistemáticos: son los que se producen siempre, suelen conservar la magnitud y el sentido, se deben a desajustes del instrumento, desgastes etc. dan lugar a sesgo en las medidas.
* Errores aleatorios: son los que se producen de un modo no regular, variando en magnitud y sentido de forma aleatoria, son difíciles de prever, y dan lugar a la falta de calidad de la medición.
Error absoluto
* El error absoluto de una medida es la diferencia entre el valor de la medida y el valor real de una magnitud (valor tomado como exacto).
Error relativo
* Es la relación que existe entre el error absoluto y la magnitud medida, es adimensional, y suele expresarse en porcentaje.
Calculo del error en medidas directas.
Una forma de calcular el error en una medida directa, es repetir numerosas veces la medida:
En este caso asignamos como valor de la medición la media aritmética de estas medidas y como error la desviación típica de estos valores.
Medidas indirectas
No siempre es posible realizar una medida directa, porque no disponemos del instrumento adecuado que necesitas tener, porque el valor a medir es muy grande o muy pequeño depende, porque hay obstáculos de otra naturaleza, etc.Medición indirecta es aquella que realizando la medición de una variable, podemos calcular otra distinta, por la que estamos interesados.
Ejemplo:
Queremos medir la altura de un edificio muy alto, dadas las dificultades de realizar la medición directamente, emplearemos un método indirecto. Colocaremos en las proximidades del edificio un objeto vertical, que sí podamos medir, así como su sombra. Mediremos también la longitud de la sombra del edificio. Dada la distancia del Sol a la tierra los rayos solares los podemos considerar paralelos, luego la relación de la sombra del objeto y su altura, es la misma que la relación entre la sombra del edificio y la suya.
- Llamaremos:
-
- So: a la sombra del objeto
- Ao: a la altura del objeto
-
- Se: a la sombra del edificio
- Ae: a la altura del edificio
Errores en las medidas indirectas
Cuando el cálculo de una medición se hace indirectamente a partir de otras que ya conocemos, que tienen su propio margen de error, tendremos que calcular junto con el valor indirecto, que suele llamarse también valor derivado, el error de éste, normalmente empleando el diferencial total. A la transmisión de errores de las magnitudes conocidas a las calculadas indirectamente se le suele llamar propagación de errores.
Calculo del error en las medidas indirectas
Partiendo de unas medidas directas y de los errores de esas medidas, y conociendo una ecuación por la que a partir de las medidas conocidas podemos calcular el valor de una medida indirecta, un método de cálculo del error de esta medida indirecta es el cálculo diferencial, equiparando los diferenciales a los errores de cada variable.En el ejemplo de la altura del edificio, tenemos tres variables independientes la sombra del edificio, la sombra del objeto y la altura del objeto, y una variable dependiente la altura del edificio que calculamos mediante las otras tres y la ecuación que las relaciona, como ya se ha visto.
Ahora calculemos el error cometido en la altura del edificio según todo lo anterior, la ecuación que tenemos es:
Donde:
 : es el error que hemos cometido al calcular la altura del edificio.
: es el error que hemos cometido al calcular la altura del edificio. : es el error de medida de la sombra del edificio.
: es el error de medida de la sombra del edificio. : es el error de medida en la altura del objeto.
: es el error de medida en la altura del objeto. : es el error de medida en la sombra del objeto.
: es el error de medida en la sombra del objeto.



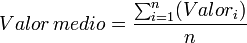

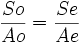

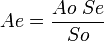






No hay comentarios:
Publicar un comentario